Quantum Computing and Public Key Cryptography

Quantum computing, despite being relatively new, is already starting to make waves in the technology industry. Computers that promise to be millions of times faster in certain computations than any supercomputer. But how will this new technology affect digital security?

First lets have an introduction at our current models in digital security.

Digital security mostly consists of cryptography and the internet and most other digital applications use a model of cryptography called Public-Key cryptography. How does this work? Generally when we want to send messages in the old days we usually encrypt the message and send this encrypted message to the recipient along with the encryption key to decrypt this. This is called Symmetric-Key cryptography, the same key is used for both encryption and decryption. But this system has a critical weakness: the key has to be sent to the receiver along with the text so an attacker can intercept this message and use the key to decrypt the message.

This is especially dangerous when the sender and the recipient have no way to meet physically so that they can decide on the key beforehand. Furthermore, once the attacker has access to the key he can use the key and
pretend he is the receiver, thus fooling both the actual sender and receiver, known as a MITM, or Man-In-The-Middle, attack.

Public-Key cryptography solves this issue known as the Key Distribution problem by using two keys, a public key known by everyone, and a private key that only the owner knows. Both of these keys are used by the sender and receiver so that the risk of an attacker gaining access is reduced significantly. The keys are generated using a very large random number along with a cryptographic or mathematical algorithm. These numbers can be hundreds of digits long.

So how does this system work in practice?

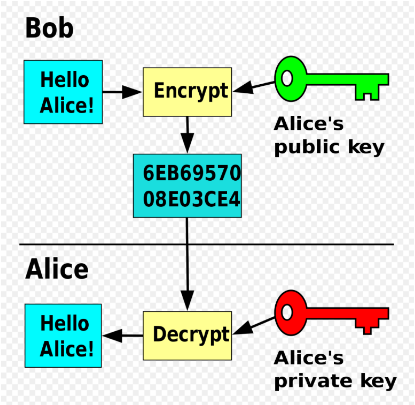
Consider the following scenario: Bob wants to send an encrypted message to Alice. So in order to do this he first encrypts the message using Alice’s public key, which is available to the public and sends the resulting text to Alice. She uses her private key and decrypts the message.

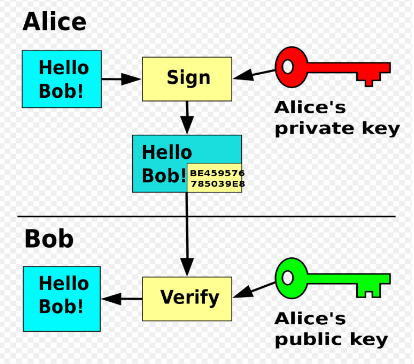
Another extension of this system is digital
signatures, which are used to verify the
sender’s or receiver’s authenticity. In the
example Alice encrypts her sign with her
private key and sends it to Bob along with
the message, which is encrypted with Bob’s
public key. Bob will then use Alice’s public
key to verify her digital signature and then
use his private key to decrypt the message.

The effectiveness of Public-Key cryptography has lead to its use in many security models today, notably Secure Socket Layer(SSL), Transport Layer Security(TLS), Pretty Good Privacy(PGP), GNU Privacy Guard(GPG), HTTPS, and many more. Public-key cryptography is slower than symmetric encryption and sometimes a combination of both is used, such as in TLS. The cryptographic algorithms used in this system are generally built on one of two math problems that are easy to verify but difficult to solve:

Why these two problems?

Its because there is no shortcut in solving these problems and their complexity is bounded exponentially meaning as the length of the numbers used increases, the problem gets exponentially harder to solve. However the solution to these can be verified quickly. So a computer can verify the keys quickly, even if they are very long, but it would take years for a supercomputer to break the encryption.

Quantum computers however change this a bit. They use quantum algorithms, notably Shor’s algorithm to compute these. It doesn’t make it able to instantly break the encryption but it makes it easier by reducing the complexity of the problems mentioned from exponential to polynomial. That doesn’t sound like much but its big.

How big?

When we talk about the problems above we can predict the number of steps a computer would take to solve it. A regular computer can solve the problem, using a number with N digits, in about 2^N steps. A quantum computer using Shor’s algorithm can solve the same problem in about N^2 steps. So for a 10 digit number a regular computer would take 2^10 or 1024 steps but a quantum computer can do it in around 10^2 or 100 steps. For a 50 digit number would take around 2500 steps for a quantum computer but a regular computer would take
trillions of steps. As N goes up the gap between the 2 computers widens exponentially.

And this is why quantum computing poses a risk to digital security. Its not easy for them to break the encryption but its not that hard either. Of course the current quantum computers are not fault-tolerant or practical enough to be used in breaking security systems yet but this field is developing faster than classical computing ever did so it won’t be long till quantum computers are powerful enough to break our current models of digital security.

What people can do right now is develop models that would resist quantum computers. Quantum computers may be faster than classical computers in certain problems but not in all problems, notably hashes.

It may be a while before our current models of digital security will become obsolete and quantum computers would lead to that but hopefully a quantum- resistant digital security model would be developed by then.

YUTHIN HIMSARA

References:http://How Quantum Computing Will Turn Digital Security Upside Down | Hacking Tutorials by Xeus (xeushack.com) http://Public-key cryptography – Wikipedia