Fibonacci

The mathematician Leonardo of Pisa, better known as Fibonacci, had a significant impact on mathematics. His contributions to mathematics have intrigued and inspired people through the centuries to delve more deeply into the mathematical world. He is best known for the sequence of numbers bearing his name. 

Fibonacci wrote several books including Liber Abaci, a geometry book and a book on number theory. It earned him recognition as a talented mathematician. The most well-known of his works is Liber Abaci, which means the book of calculating or the book of computation. This book was quite possibly one of the most influential mathematical works of the Middle Ages.

Origin of the sequence

Despite his influential contributions to European mathematics, Fibonacci is most remembered for a single sequence of numbers that provided the solution to a problem included in Liber Abaci. Like most of the problems in the book, Fibonacci did not invent this problem himself, but his solution to it has forever immortalized him in the mathematical world.

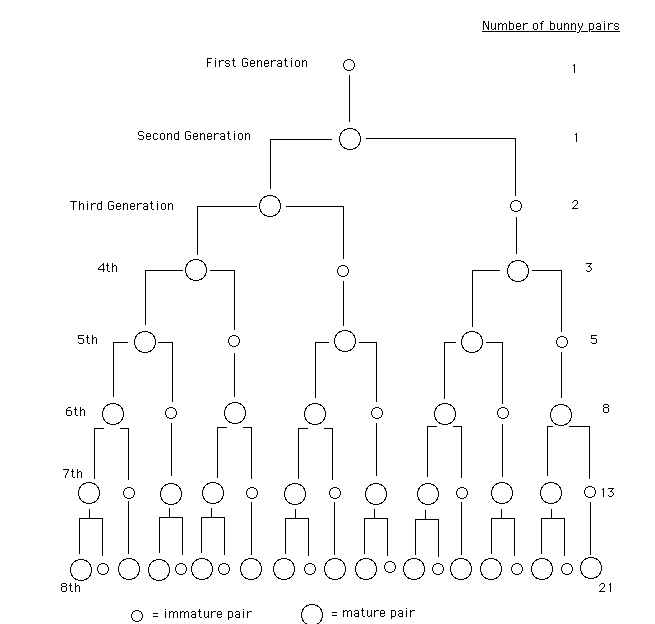
The problem, dealing with the regeneration of rabbits, calculated the number of rabbits after a year if there is only one pair the first month. The problem states that it takes one month for a rabbit pair to mature, and the couple will then produce one pair of rabbits each following month.

Fibonacci’s solution stated that in the first month there would be only one pair; the second month there would be an adult pair and a baby pair; the third month there would be two adult pairs and one baby pair; and so forth. When the total number of rabbits for each month is listed, one after the other, it generates the Fibonacci Sequence;

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233

Patterns and Properties of the Fibonacci Sequence

In this sequence, each term is obtained by adding the two preceding terms. The Fibonacci sequence is the oldest known recursive sequence, which is a sequence where each successive term can only be found through performing operations on previous terms. Interestingly, Fibonacci does not comment on the recursive nature of this sequence.

This relationship was not identified in any publication until four hundred years later. At the time of the publication of Liber Abaci, no special notice was taken of these numbers. It was not until the mid-1800s that mathematicians began to be intrigued by what would later be known as the Fibonacci numbers.

A closer inspection of the Fibonacci numbers brings to light all sorts of fascinating patterns and mathematical properties. Fibonacci himself makes no mention of them in his book, but the following patterns are a few that have been brought to light over years of examination of the numbers in the sequence.

Any two consecutive Fibonacci numbers are relatively prime, having no factors in common with each other. For example:

5, 8, 13, 21, 34,

For the following part of the sequence;

5 = 1 x 5

8 = 2 x 2 x 2

13 = 1 x 13

21 = 3 x 7

34 = 2 x 17

Summing together any ten consecutive Fibonacci numbers will always result in a number which is divisible by eleven

1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143

143 / 11 = 13

89 + 144 + 233 + 377 + 610 + 987 + 1597 + 2584 + 4181 + 6675 = 17567

17567 / 11 = 1597

Following tradition, Fn is used to represent the n-th Fibonacci number in the sequence.

n	Fn
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144
13	233

Every third Fibonacci number is divisible by F₃. Every fourth Fibonacci number is divisible by F₄. Every fifth Fibonacci number is divisible by F₅, and the pattern continues. In general, every nth Fibonacci number is divisible by the nth number in the Fibonacci sequence.

The reciprocal of the eleventh Fibonacci number, 89, can be found by adding the Fibonacci sequence in such a fashion that each Fibonacci number contributes one digit to the repeating decimal of 1/89;

Summing any number of consecutive Fibonacci numbers will result in a number that is one less than the Fibonacci number two places beyond the last one added

… 1, 1, 2, 3, 5, 8, 13 …

F₁ + F₂ + F₃ + F₄ + F₅ = 1+1+2+3+5 = 12 = 13-1 = F₇ -1

This gives a general formula for a simple way to find the sum of any number of Fibonacci number

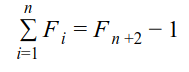
Discovering the value of a Fibonacci number given its location in the sequence can be very time consuming and tedious, particularly if it has a later placement in the sequence. Finding the fifth Fibonacci number is not difficult. Finding the fiftieth is much more cumbersome, as the process involves finding and summing the previous forty-nine terms. 

In 1843, the French mathematician Jacques-Philippe-Marie Binet discovered a formula that finds any Fibonacci number without calculating the previous numbers in the sequence. This formula finds the n^th Fibonacci number using a number called the golden ratio, 𝛷, and its inverse:

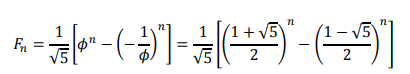
Where does it appear? Is this sequence important?

Now let’s look at another reasonably natural situation where the same sequence mysteriously pops up. Go back 350 years to 17th century France. Blaise Pascal, a young French scholar, is consulted by a friend, a professional gambler, the Chevalier de Mé ré, Antoine Gombaud. The Chevalier asks Pascal some questions about plays at dice and cards and the proper division of the stakes in an unfinished game. Pascal responded by inventing an entirely new branch of mathematics, the theory of probability. This theory has grown over the years into a vital 20th-century tool for science and social science. His work leans heavily on a collection of numbers now called the Pascal’s triangle, and represented like this:

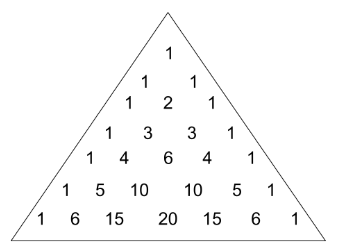
Now for visual convenience draw the triangle left-justified. Add up the numbers on the various diagonals …

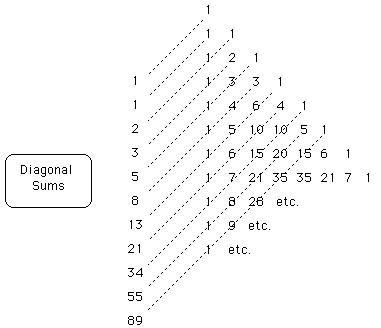
… and we get the fibonacci sequence!!

Applications

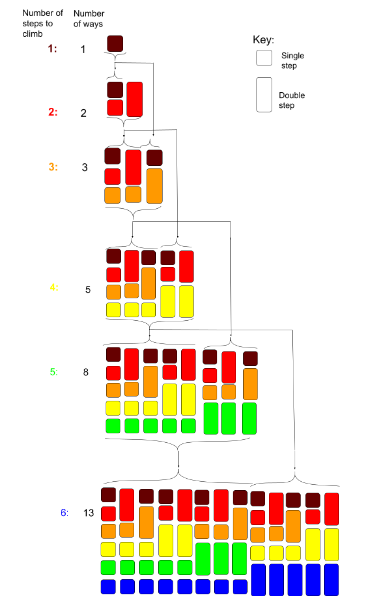
The Fibonacci numbers give the solution to certain enumerative problems, the most common of which is that of counting the number of ways of writing a given number n as an ordered sum of 1s and 2s (called compositions). There are Fn+1 ways to do this. For example, there are F5+1 = F6 = 8 ways one can climb a staircase of 5 steps, taking one or two steps at a time:

5 = 1+1+1+1+1 = 2+1+1+1 = 1+2+1+1 = 1+1+2+1 = 2+2+1

   = 1+1+1+2 = 2+1+2 = 1+2+2

The figure shows that 8 can be decomposed into 5 (the number of ways to climb 4 steps, followed by a single-step) plus 3 (the number of ways to climb 3 steps, followed by a double-step). The same reasoning is applied recursively until a single step, of which there is only one way to climb.

Below are few application of Fibonacci Numbers in Computer science:

1. The Fibonacci numbers are important in the computational run-time analysis of Euclid’s algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.
2. Fibonacci numbers are used in a polyphase version of the merge sort algorithm. In this algorithm, an unsorted list is split into two lists whose lengths correspond to sequential Fibonacci numbers so that the two parts of the list have lengths in the approximate proportion to φ. The Art of Computer Programming describes a tape-drive implementation of the polyphase merge sort.
3. Some pseudorandom number generators use these numbers.
4. Fibonacci numbers arise in the analysis of the Fibonacci heap data structure.
5. A one-dimensional optimization method, called the Fibonacci search technique, uses Fibonacci numbers too.
6. Raghu and Ravishankar(2015) developed a paper on applying classical encryption techniques for securing data. Raphael and Sundaram(2012) showed that communication may be secured by the use of Fibonacci numbers.

Appearance in Nature

Interestingly, the pattern of growth of the sequence matches the forces controlling growth in a large variety of natural dynamical systems in some mysterious way. Quite analogous to the reproduction of rabbits, let us consider the family tree of a bee – so we look at ancestors rather than descendants. In a simplified reproductive model, male bees hatch from unfertilized eggs while females hatch from fertilized eggs. Hence a male has only one parent while a female has two. Here is the family tree of a typical male bee:

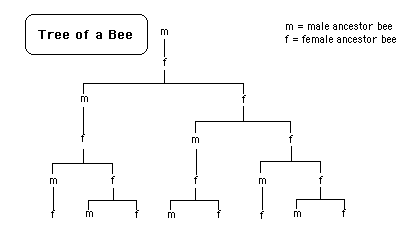
Notice that this looks like the bunny chart but moves backwards in time. The male ancestors, female ancestors and the total in each generation form a

Fibonacci sequence. You can see from the tree that bee society is female-dominated.

The most beautiful examples of the occurrence of the Fibonacci sequence in nature are found in a variety of trees and flowers, generally associated with some spiral structure. For instance, leaves on the stem of a flower or a tree branch often grow in a helical pattern, spiralling around the branch as new leaves form further away. 

Look at a branch and focus your attention on a given leaf and start counting around and outwards. Count the leaves and the number of turns around the branch, until you return to a position matching the original leaf but further along the branch. Generally, both are Fibonacci numbers.

Give below are few trees that have this pattern;

Tree	Leaves	Turns
Elm	2	1
Cherry	3	2
Beech	3	1
Poplar	5	2
Weeping willow	8	3
Pear	8	3
Almond	13	8

You can take a walk in a park and find this pattern on plants and bushes quite easily. Many flowers offer a beautiful confirmation of the Fibonacci mystique. A daisy has a central core consisting of tiny florets arranged in opposing spirals. There are usually 21 going to the left and 34 to the right. A mountain aster may have 13 spirals to the left and 21 to the right. Sunflowers are the most spectacular example, typically having 55 spirals one way and 89 in the other.

Pine cones, too, are constructed in a spiral fashion. Commonly, small ones have 8 spirals one way and 13 the other. The most interesting is the pineapple – built from adjacent hexagons, three kinds of spirals appear in three dimensions. There are 8 to the right, 13 to the left, and 21 vertically – a Fibonacci triple

Why should this be? Why has Mother Nature found an evolutionary advantage in arranging plant structures in spiral shapes exhibiting the Fibonacci sequence?

We have no proven answer. In 1875, a mathematician named Wiesner provided a mathematical demonstration that the spiral arrangement of leaves on a branch in Fibonacci proportions was an efficient way to gather a maximum amount of sunlight with a few leaves – he claimed, the best way. But recently, a Cornell University botanist named Karl Niklas decided to test this hypothesis in his laboratory; he discovered that almost any reasonable arrangement of leaves has the same sunlight-gathering capability. So we are still in the dark about light.

However, Dan Reich, an associate professor at Temple University, thinks we can begin to understand the presence of spirals and their connection with the Fibonacci sequence.Spirals arise from a property of growth called self-similarity or scaling – the tendency to grow in size while maintaining the same shape. Not all organisms grow in this self-similar manner. We can see that adult people, for example, are not just scaled up babies: babies have larger heads, shorter legs, and a longer torso relative to their size. However, a nautilus exhibits self-similar growth. As the nautilus outgrows each chamber, it builds new chambers for itself, always the same shape. If you imagine a very long-lived nautilus, its shell will spiral around and around, growing ever larger but always looking the same at every scale.

Here is where Fibonacci comes in – we can build a squarish sort of nautilus by starting with a unit square and successively building on new rooms whose size correspond to the Fibonacci sequence:

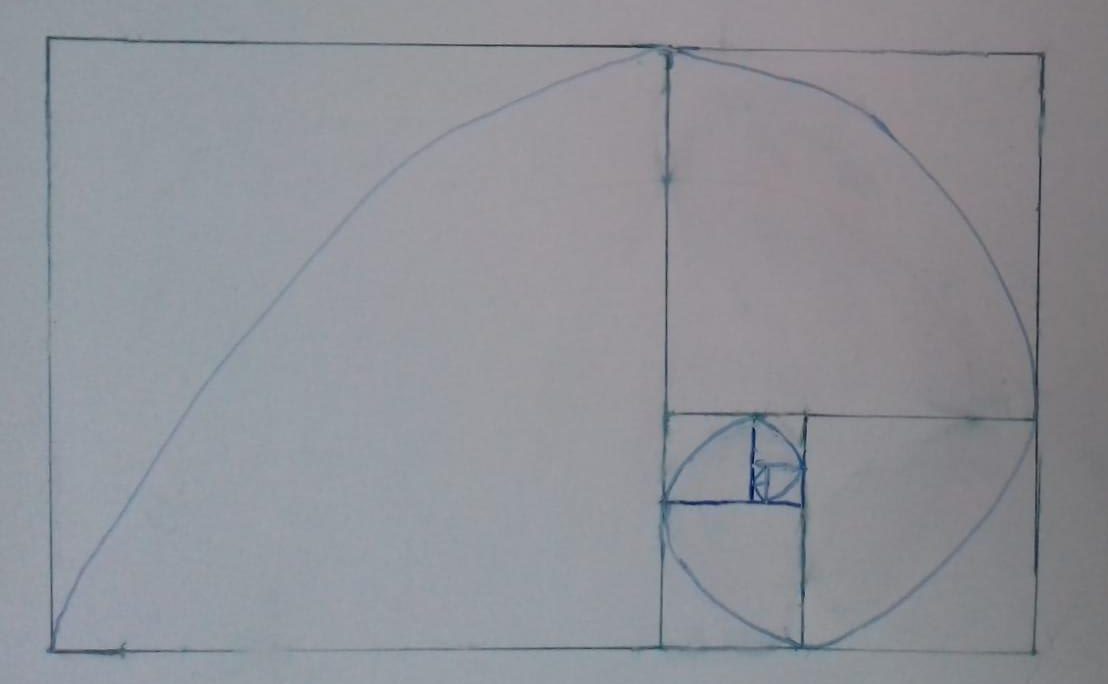
Running through the centres of the squares in order, with a smooth spiral, we obtain the nautilus spiral = the sunflower spiral. It is a self-similar curve that keeps its shape at all scales (if you imagine it spiralling out forever). It is equiangular because a radial line from the centre always makes the same angle to the curve.

 As the spiral is self-similar, it looks the same at every scale. Hence, the scale does not matter. What matters is the proportion. These spirals have a fixed ratio determining their shape. It turns out that this proportion is the same

as the proportions generated by successive entries in the Fibonacci sequence: 5:3, 8:5,13:8, and so on. Here is the calculation:

Fibonacci Proportions

The sequence of terms (fn)	Ratios of successive terms(fn/fn-1)(non-exact decimals given to 7d.p.)
1	–
1	1
2	2
3	1.5
5	1.6666666…
8	1.6
13	1.625
21	1.6153846…
34	1.6190476…
55	1.6176470…
89	1.6181818…
144	1.6179775…
233	1.6180555…
377	1.6180257…
610	1.6180371…

As we go further in the sequence, the proportions of adjacent terms begin to approach a fixed limiting value of 1.6180339…, the Golden Mean of Euclid and Aristotle. It is the divine proportion of Leonardo DaVinci, considered the most beautiful and significant of quantities, with a long honoured history. This number has more tantalizing properties than you can imagine.

In conclusion the Fibonacci sequence is a recursive sequence which has a simple definition: fn = fn-1 + fn-2. However, it has many interesting properties and appears in nature mysteriously. The Fibonacci sequence fits into three main reasons we learn math as mentioned in the YouTube video. It has calculation in its patterns and definition. It has inspiration due to its mysterious appearance in nature and its wonderful patterns. Most importantly, it has many applications in computer science and other fields. Hope this article gave you insight on the beauty of mathematics.

Credits

https://www.quora.com/What-is-the-scientific-importance-of-Fibonacci-series

https://math.temple.edu/~reich/Fib/fibo.html

https://core.ac.uk/download/pdf/58824887.pdf

https://www.researchgate.net/publication/330740074_The_Fibonacci_Numbers_and_Its_Amazing_Applications

https://www.bbc.co.uk/sounds/play/b008ct2j

By Inesh Palihapitiya